瀏覽標籤：

遞迴

[C#][LeetCode][Easy] 226. Invert Binary Tree

作者lex.xu
/
1 月 09, 2017
/
心得筆記

心得：

這題也是典型的遞迴，題目要求把二元樹整個翻轉過來。

問題：

Invert a binary tree.

     4
   /   \
  2     7
 / \   / \
1   3 6   9

     4
   /   \
  7     2
 / \   / \
9   6 3   1

答案：

遞迴

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int x) { val = x; }
 * }
 */
public class Solution {
    public TreeNode InvertTree(TreeNode root) {
        if(root == null){
            return null;
        }
        
        var left = root.left;
        var right = root.right;
        root.left = InvertTree(right);
        root.right = InvertTree(left);
        
        return root;
    }
}

[C#][LeetCode][Easy] 258. Add Digits

作者lex.xu
/
1 月 08, 2017
/
心得筆記

心得：

題目要求將每一位數相加，直到剩下個位數。

問題：

Given a non-negative integer num, repeatedly add all its digits until the result has only one digit.

For example:

Given num = 38, the process is like: 3 + 8 = 11, 1 + 1 = 2. Since 2 has only one digit, return it.

答案：

For + 遞迴

public class Solution {
    public int AddDigits(int num) {
        string str = num.ToString();
        if (str.Length < 2)
        {
            return int.Parse(str);
        }
        else
        {
            int tmp = 0;
            for (int i = 0; i < str.Length; i++)
            {
                tmp += int.Parse(str[i].ToString());
            }
    
            return AddDigits(tmp);
        }
    }
}

LinQ + 遞迴

public class Solution {
    public int AddDigits(int num) {
        string str = num.ToString();
        if (str.Length < 2)
        {
            return int.Parse(str);
        }
        else
        {
            return AddDigits(str.Sum(x => int.Parse(x.ToString())));
        }
    }
}

Normal

public class Solution {
    public int AddDigits(int num) {
        string str = num.ToString();
        while (str.Length > 1)
        {
            int tmp = 0;
            for (int i = 0; i < str.Length; i++)
            {
                tmp += int.Parse(str[i].ToString());
            }

            str = tmp.ToString();
        }

        return int.Parse(str);
    }
}

[C#][LeetCode][Easy] 104. Maximum Depth of Binary Tree

作者lex.xu
/
1 月 05, 2017
/
心得筆記

心得：

這題是典型的遞迴題目，題目要求找到二元樹最深的層級為多少。

這題的解法很簡單，先宣告兩個變數分別來儲存左邊與右邊的層級，首先判斷左邊是否為空，若非為空值則會繼續搜尋此節點的子節點是否為空，搜尋完畢後再一併回傳至第一層的left變數裡，右邊反之，最後在比較左右兩邊哪個最大，最大的數字即為二元樹的層級。

問題：

Given a binary tree, find its maximum depth.

The maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

答案：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int x) { val = x; }
 * }
 */
public class Solution {
    public int MaxDepth(TreeNode root) {
        if (root == null)
        {
            return 0;
        }

        int left = 1;
        int right = 1;

        if (root.left != null)
        {
            left += MaxDepth(root.left);
        }

        if (root.right != null)
        {
            right += MaxDepth(root.right);
        }

        return right > left ? right : left;
    }
}

參考：

https://skyyen999.gitbooks.io/-leetcode-with-javascript/content/questions/104md.html

[C#] 基礎複習 – 遞迴練習

作者lex.xu
/
1 月 05, 2017
/
心得筆記

好久沒用遞迴了，趕快找個簡單的題目複習一下，不然都要忘光光了，熟悉一下之前的Feel ~
順便練習一下簡單工廠模式，首先設計介面ICompute.cs：

interface ICompute
{
    /// <summary>
    /// 1 + ... + N = ?
    /// </summary>
    /// <param name="n"></param>
    /// <returns>Answer</returns>
    Int64 Iterative(Int64 n);

    /// <summary>
    /// 1 - 2 + 3 ... + N = ?
    /// </summary>
    /// <param name="n"></param>
    /// <returns>Answer</returns>
    Int64 AdvancedIterative(Int64 n);

    /// <summary>
    /// 1 x 2 x ... x N = ?
    /// </summary>
    /// <param name="n"></param>
    /// <returns>Answer</returns>
    Int64 Factorial(Int64 n);

    /// <summary>
    /// Fn = Fn-1 + Fn-2
    /// </summary>
    /// <param name="n"></param>
    /// <returns>Answer</returns>
    Int64 Fibonacci(Int64 n);
}

接著建立兩個類別Recursive.cs與ForLoop.cs並繼承ICompute.cs實作其方法：

Recursive.cs

public class Recursive : ICompute
{
    public Int64 Iterative(Int64 n)
    {
        if (n == 1)
        {
            return n;
        }
        else
        {
            return n + Iterative(n - 1);
        }
    }

    public Int64 AdvancedIterative(Int64 n)
    {
        if (n == 1)
        {
            return n;
        }
        else
        {
            return n % 2 == 0 ? -n + AdvancedIterative(n - 1) : n + AdvancedIterative(n - 1);
        }
    }

    public Int64 Factorial(Int64 n)
    {
        if (n == 1)
        {
            return n;
        }
        else
        {
            return n * Factorial(n - 1);
        }
    }

    public Int64 Fibonacci(Int64 n)
    {
        if (n < 3)
        {
            return 1;
        }
        else
        {
            return Fibonacci(n - 1) + Fibonacci(n - 2);
        }
    }
}

ForLoop.cs

public class ForLoop : ICompute
{

    public Int64 Iterative(Int64 n)
    {
        int ans = 0;

        for (int i = 1; i <= n; i++)
        {
            ans += i;
        }

        return ans;
    }

    public Int64 AdvancedIterative(Int64 n)
    {
        int ans = 0;

        for (int i = 1; i <= n; i++)
        {
            if (i % 2 == 0)
            {
                ans -= i;
            }
            else
            {
                ans += i;
            }
        }

        return ans;
    }

    public Int64 Factorial(Int64 n)
    {
        int ans = 1;

        for (int i = 1; i <= n; i++)
        {
            ans *= i;
        }

        return ans;
    }

    public Int64 Fibonacci(Int64 n)
    {
        int ans = 0;
        int[] arr = new int[2] { 1, 1 };

        for (int i = 1; i <= n; i++)
        {
            if (i < 3)
            {
                ans = 1;
            }
            else
            {
                ans = arr[0] + arr[1];
                arr[0] = arr[1];
                arr[1] = ans;
            }
        }

        return ans;
    }
}

接著在Program.cs裡面寫一個Run的方法來呼叫剛剛寫好的兩個類別：

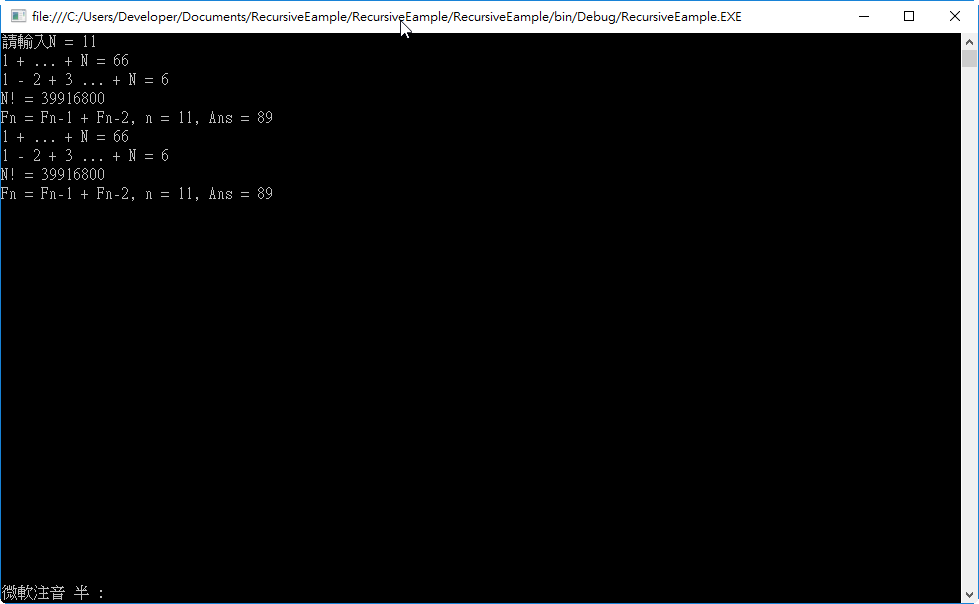
static void Run(int n, ICompute compute)
{
    Console.WriteLine("1 + ... + N = {1}", n, compute.Iterative(n));
    Console.WriteLine("1 - 2 + 3 ... + N = {1}", n, compute.AdvancedIterative(n));
    Console.WriteLine("N! = {1}", n, compute.Factorial(n));
    Console.WriteLine("Fn = Fn-1 + Fn-2, n = {0}, Ans = {1}", n, compute.Fibonacci(n));
}

這樣就完成囉 !!

原始碼：https://github.com/shuangrain/RecursiveEample